Batch 2 - Class 46 - Pigeon Hole Principle
Preclass Exercise:
- Dudeney - 162: Can you cut this chain out of a piece of thick cardboard without any join whatever? Every link is solid; without its having been split and afterwards joined at any place.
.png) Answer: The reader will probably feel rewarded for any care and patience that he may bestow on cutting out the cardboard chain. We will suppose that he has a piece of cardboard measuring 8 in. by 2½ in., though the dimensions are of no importance. Yet if you want a long chain you must, of course, take a long strip of cardboard. First rule pencil lines B B and C C, half an inch from the edges, and also the short perpendicular lines half an inch apart. Rule lines on the other side in just the same way, and in order that they shall coincide it is well to prick through the card with a needle the points where the short lines end. Now take your penknife and split the card from A A down to B B, and from D D up to C C. Then cut right through the card along all the short perpendicular lines, and half through the card along the short portions of B B and C C that are not dotted. Next turn the card over and cut half through along the short lines on B B and C C at the places that are immediately beneath the dotted lines on the upper side. With a little careful separation of the parts with the penknife, the cardboard may now be divided into two interlacing ladder-like portions, as shown in Fig. 2; and if you cut away all the shaded parts you will get the chain, cut solidly out of the cardboard, without any join. It is an interesting variant of the puzzle to cut out two keys on a ring—in the same manner without join.
Answer: The reader will probably feel rewarded for any care and patience that he may bestow on cutting out the cardboard chain. We will suppose that he has a piece of cardboard measuring 8 in. by 2½ in., though the dimensions are of no importance. Yet if you want a long chain you must, of course, take a long strip of cardboard. First rule pencil lines B B and C C, half an inch from the edges, and also the short perpendicular lines half an inch apart. Rule lines on the other side in just the same way, and in order that they shall coincide it is well to prick through the card with a needle the points where the short lines end. Now take your penknife and split the card from A A down to B B, and from D D up to C C. Then cut right through the card along all the short perpendicular lines, and half through the card along the short portions of B B and C C that are not dotted. Next turn the card over and cut half through along the short lines on B B and C C at the places that are immediately beneath the dotted lines on the upper side. With a little careful separation of the parts with the penknife, the cardboard may now be divided into two interlacing ladder-like portions, as shown in Fig. 2; and if you cut away all the shaded parts you will get the chain, cut solidly out of the cardboard, without any join. It is an interesting variant of the puzzle to cut out two keys on a ring—in the same manner without join.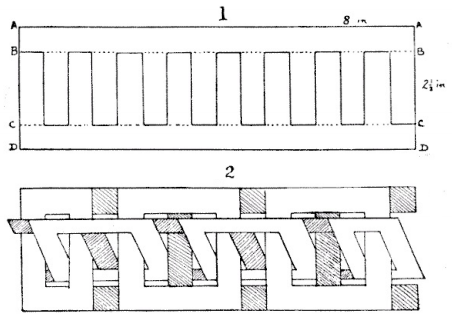

Attendance: Tishyaa, Smiti, Diya, Muskaan, Rhea, Avy, Arnav, Kabir, Shubham, Anisha, Liza, Nandini, Hriday, Aastha, Adit, Diya
Class Notes:
(MC - Chapter 4)
Explain basic Pigeonhole principle: If we put N+1 or more pigeons into N pigeon holes, then some pigeon hole must contain two or more pigeons.
- A bag contains beads of two colors: black and white. What is the smallest number of beads which must be drawn so that there are two of the same color?Answer: 3 - Explain in terms of what is the pigeon and what is the pigeon hole
- One million pine trees grow in a forest. Each pine tree has up to 600,000 needles on it. Show that at least two pine tress must have the same number of needlesExplain in terms of pigeon and pigeon hole(Hav 2007) - People are seated around a circular table at a restaurant. The food is placed on a circular platform in the center of the table and this circular platform can rotate. Each person ordered a different entrée, and it turns out that no one has the correct entrée in front of him. Show that it is possible to rotate the platform so that at least two people will have the correct entréeNumber of rotations (n-1), number of matches n, hence at least two in one. Explain in terms of pigeons and pigeon holes.Given twelve integers, show that two of them can be chosen whose difference is divisible by 11Can you generalize to n numbers? What is the pigeon and what is the pigeon hole?
- (Dudeney - 99) "A man I know," said Teddy Nicholson at a certain family party, "possesses a string of thirty-three pearls. The middle pearl is the largest and best of all, and the others are so selected and arranged that, starting from one end, each successive pearl is worth £100 more than the preceding one, right up to the big pearl. From the other end the pearls increase in value by £150 up to the large pearl. The whole string is worth £65,000. What is the value of that large pearl?"Answer: £3,000
Homework:
- MartinShCol - 1.15 - In a line up of 10 soldiers, what is the least number of soldiers that can be picked in order of either ascending or descending heights? Assume that no two soldiers have the same height.
References:
https://ia902701.us.archive.org/4/items/AmusementsInMathematicspdf/AmusementsInMathematics.pdf - Dudeney
Mathematical Circles (Russian Experience), by Dmitri Fomin, Sergey Genkin, Ilia Itenberg
Haverford College Problem Solving group - http://blogs.haverford.edu/mathproblemsolving/files/2010/05/4.2-Pigeonhole-Solutions.pdf?file=2010/05/4.2-Pigeonhole-Solutions.pdf
The Colossal Book of Short Puzzles and Problems, by Martin Gardner
- MartinShCol - 1.23 (a) (rotating roundtable - do with 6 people)